図表32 目標コーホートの結婚出生力低下係数(k)の仮定
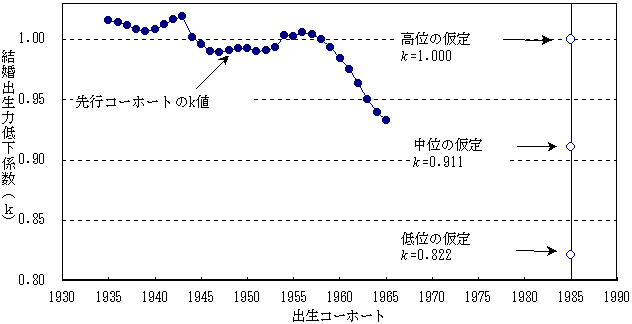
図表33-2 仮定された女子1985年コーホートの合計特殊出生率および出生児数分布
| 仮定の種類 |
生涯未婚率 |
平均初婚
年齢 |
修正夫婦完結出生児数 |
離死別
効果係数 |
コーホート合計
特殊出生率 |
| |
夫婦完結
出生児数 |
結婚出生力
低下係数 |
| 中位 |
16.8 |
27.8 |
1.72 |
1.89 |
0.911 |
0.971 |
1.39 |
| 高位 |
13.3 |
27.3 |
1.93 |
1.93 |
1.000 |
0.971 |
1.62 |
| 低位 |
22.6 |
28.7 |
1.49 |
1.81 |
0.822 |
0.971 |
1.12 |
図表33-2 仮定された女子1985年コーホートの合計特殊出生率および出生児数分布
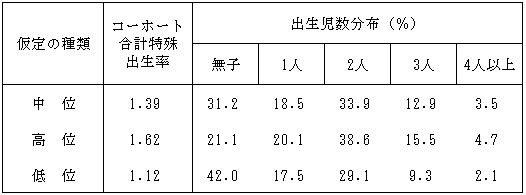
図表34 出生コーホート別にみた年齢別出生率：実績値およびモデル値
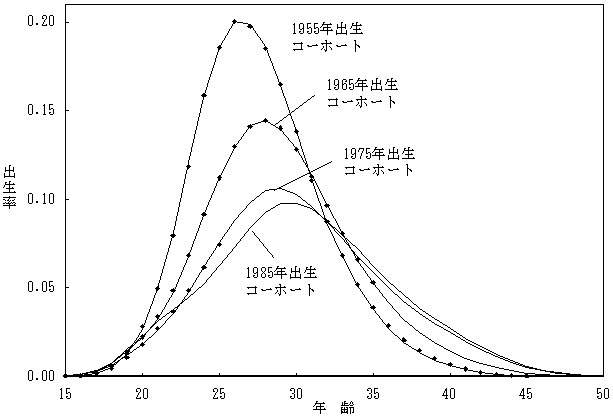
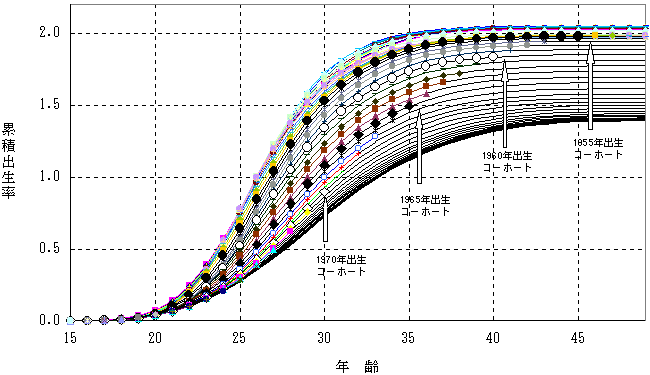
図表35-1 年齢別にみた出生コーホートの累積出生率：中位の仮定にもとづく
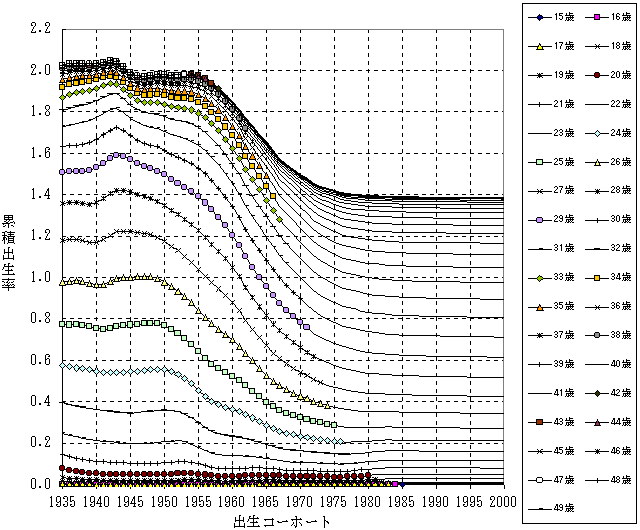
図表35-2 出生コーホート別にみた年齢累積出生率：中位の仮定にもとづく
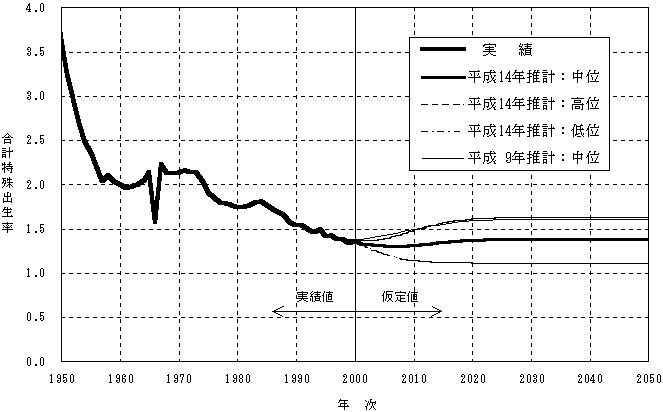
図表36 合計特殊出生率の年次推移：実績値および仮定値
|
図表37 仮定された合計特殊出生率の推移
| 年次 |
中位 |
高位 |
低位 |
|
年次 |
中位 |
高位 |
低位 |
| 平成12 (2000) |
1.36009 |
1.36009 |
1.36009 |
|
|
|
|
| 13 (2001) |
1.34277 |
1.36761 |
1.31671 |
平成38 (2026) |
1.38214 |
1.62256 |
1.10603 |
| 14 (2002) |
1.33240 |
1.36752 |
1.29344 |
39 (2027) |
1.38253 |
1.62303 |
1.10527 |
| 15 (2003) |
1.32344 |
1.37084 |
1.26896 |
40 (2028) |
1.38304 |
1.62348 |
1.10475 |
| 16 (2004) |
1.31686 |
1.37857 |
1.24511 |
41 (2029) |
1.38361 |
1.62391 |
1.10441 |
| 17 (2005) |
1.31076 |
1.38831 |
1.22074 |
42 (2030) |
1.38420 |
1.62429 |
1.10419 |
| 18 (2006) |
1.30696 |
1.40118 |
1.19843 |
43 (2031) |
1.38477 |
1.62460 |
1.10404 |
| 19 (2007) |
1.30622 |
1.41744 |
1.17963 |
44 (2032) |
1.38528 |
1.62485 |
1.10392 |
| 20 (2008) |
1.30816 |
1.43632 |
1.16432 |
45 (2033) |
1.38565 |
1.62496 |
1.10375 |
| 21 (2009) |
1.31166 |
1.45585 |
1.15156 |
46 (2034) |
1.38599 |
1.62505 |
1.10363 |
| 22 (2010) |
1.31786 |
1.47677 |
1.14260 |
47 (2035) |
1.38629 |
1.62514 |
1.10356 |
| 23 (2011) |
1.32471 |
1.49694 |
1.13555 |
48 (2036) |
1.38654 |
1.62521 |
1.10351 |
| 24 (2012) |
1.33225 |
1.51606 |
1.13025 |
49 (2037) |
1.38673 |
1.62526 |
1.10347 |
| 25 (2013) |
1.33929 |
1.53359 |
1.12556 |
50 (2038) |
1.38688 |
1.62530 |
1.10344 |
| 26 (2014) |
1.34688 |
1.55023 |
1.12258 |
51 (2039) |
1.38699 |
1.62533 |
1.10342 |
| 27 (2015) |
1.35370 |
1.56484 |
1.12022 |
52 (2040) |
1.38708 |
1.62535 |
1.10340 |
| 28 (2016) |
1.36028 |
1.57793 |
1.11880 |
53 (2041) |
1.38714 |
1.62536 |
1.10339 |
| 29 (2017) |
1.36509 |
1.58814 |
1.11677 |
54 (2042) |
1.38718 |
1.62537 |
1.10339 |
| 30 (2018) |
1.36881 |
1.59634 |
1.11469 |
55 (2043) |
1.38721 |
1.62538 |
1.10338 |
| 31 (2019) |
1.37303 |
1.60418 |
1.11407 |
56 (2044) |
1.38723 |
1.62538 |
1.10338 |
| 32 (2020) |
1.37522 |
1.60924 |
1.11222 |
57 (2045) |
1.38725 |
1.62538 |
1.10338 |
| 33 (2021) |
1.37673 |
1.61295 |
1.11039 |
58 (2046) |
1.38725 |
1.62538 |
1.10338 |
| 34 (2022) |
1.37890 |
1.61674 |
1.10983 |
59 (2047) |
1.38726 |
1.62538 |
1.10338 |
| 35 (2023) |
1.37992 |
1.61885 |
1.10857 |
60 (2048) |
1.38726 |
1.62538 |
1.10338 |
| 36 (2024) |
1.38091 |
1.62060 |
1.10769 |
61 (2049) |
1.38726 |
1.62538 |
1.10338 |
| 37 (2025) |
1.38191 |
1.62208 |
1.10713 |
62 (2050) |
1.38726 |
1.62538 |
1.10338 |
|
注：平成12(2000)年は実績値である。 |
図表38-1 生命表のリレーショナルモデル
|
(1) 生命表のリレーショナルモデルは、経験的生命表から得られた生命表関数のパラメータを用いて一連の生命表の関係を記述する方法である。
(2) 将来生命表では、特定人口の過去の生命表にもとづき、一連の生命表の関係を記述するリレーショナルモデルを作成する。そして、リレーショナルモデルのパラメータの将来値を推定することにより、将来の任意の時点の生命表を作成する。
(3) 本推計では、リー・カーターによって開発されたリレーショナルモデルを日本に適用し、男女別将来生命表を作成する。
|
図表38-2 リー・カーター・モデルの概要
|
リー・カーター・モデルは、年齢をx、時間をtとしたとき、次式により定式化される。
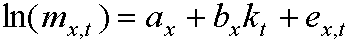
ただし、
|
図表38-3 日本人女子の生命表から得られた年齢別死亡率モデルのaxおよびbx
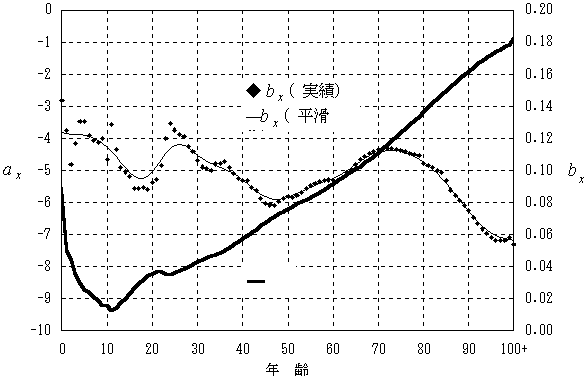
図表39 日本人女子の生命表から得た死亡の一般的水準kt ：実績値および将来値
|
１）期間別にみた kt の実績値の推移
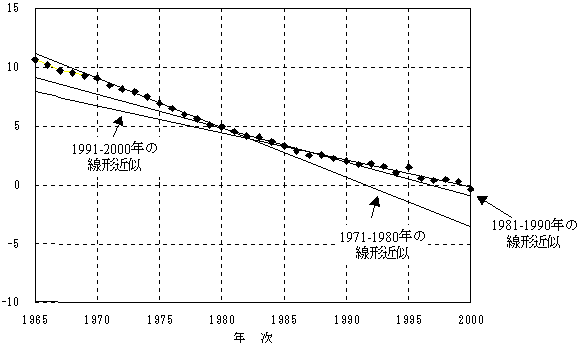
２）関数あてはめによる kt の将来値の推定
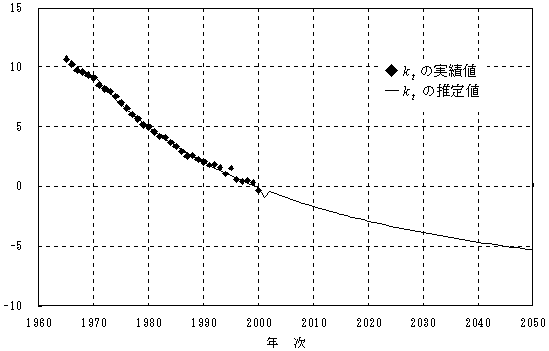
| 注： |
kt の推定に用いた関数は、次式である。
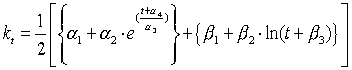
この関数は、対数関数と修正指数関数の平均である。2001年は別途推定した。
|
|
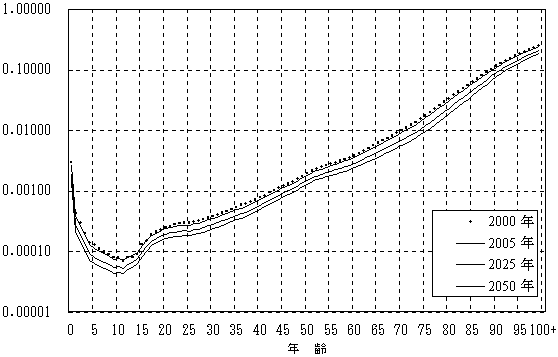
図表40 推定された将来の年齢別死亡確率（qx ）
|
１） 男子
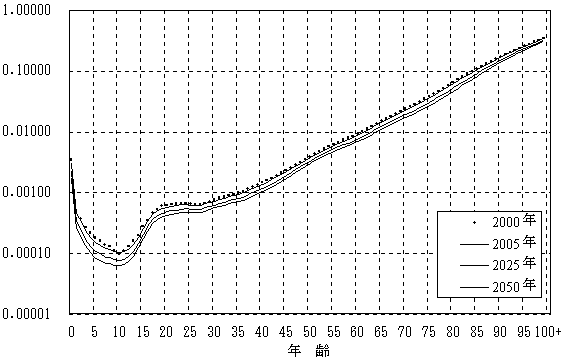
２）女子
|
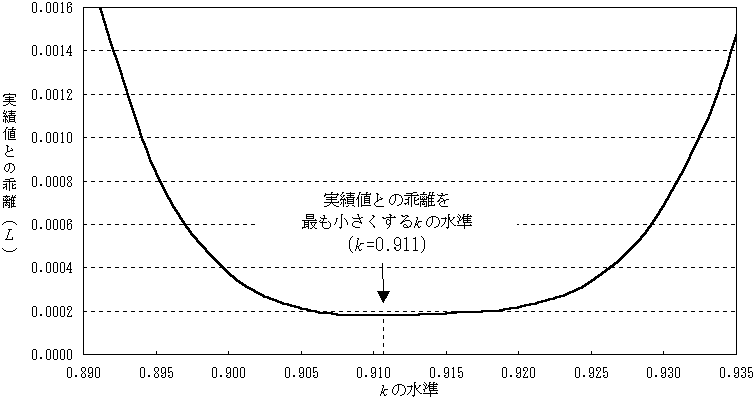
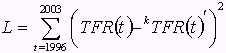
はt年における合計特殊出生率の実績値、
は異なるk値を用いたt年のモデル値。図は4次関数による近似。