勤労者３人世帯における変曲点の導出

【消費支出額の傾向から設ける仮定】

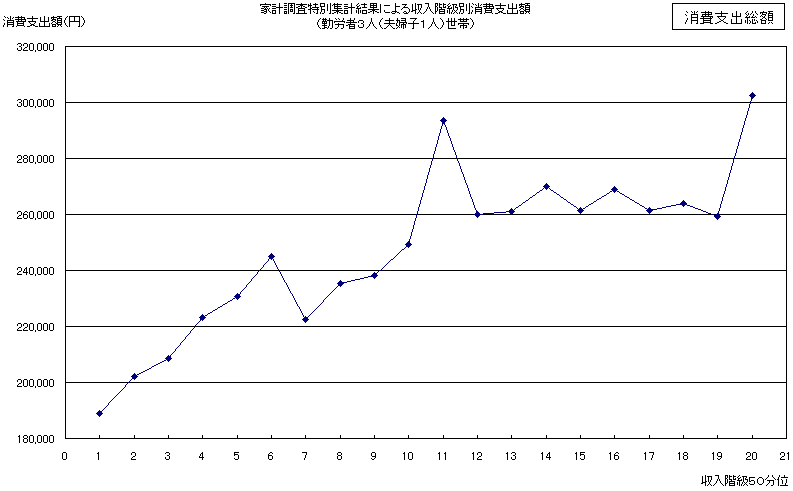
○	勤労者３人世帯（夫婦子１人世帯）における収入階級別にみた消費支出額に係るグラフは次頁図１のとおりである。
○	消費支出額の傾向から、変曲点が第３／５０分位〜第５／５０分位付近に存在するものと仮定する。　※注１

【変曲点及び消費支出額の算出】

○	第３／５０分位、第４／５０分位、第５／５０分位とそれぞれ仮定した場合における変曲点及び消費支出額の算出については右記のとおりである。　※注２

（注１）	また、第１２／５０分位を上回ると、消費支出額は暫くほぼ同じ額で推移する傾向がみられることから、これ以降の分位では傾向が異なるものと考えて、第３〜第５／５０分位から第１２／５０分位が同じ傾向を有していると仮定する。
（注２）	ここでは、上記で設定された第３〜第５／５０分位以下及び第３〜第５／５０分位から第１２／５０分位の間で推計した相関式を連立方程式とし、ここから両者の交点を求め、これを変曲点における分位とする。

［ 変曲点の算出結果 ］

変曲点が存在すると 仮定した分位	第３／５０分位	第４／５０分位	第５／５０分位
変曲点における分位	３．７０／50分位	３．６１／50分位	３．３２／50分位
変曲点における消費 支出額	216,746 円	217,901 円	214,096 円

（参考）

＜第３／５０分位付近で変曲点が存在すると仮定した場合＞

1 〜 3/50分位	ｙ ＝ 9,892.5	ｘ ＋	180,118	（ 相関係数 ＝ 0.9607 ）
3 〜 12/50分位	ｙ ＝ 6,297.5	ｘ ＋	193,429	（ 相関係数 ＝ 0.6466 ）
3,595.0		ｘ ＝	13,311
		ｘ ＝	3.70
よって		ｙ ＝	216,746

＜第４／５０分位付近で変曲点が存在すると仮定した場合＞

1 〜 4/50分位	ｙ ＝ 10,975	ｘ ＋	178,315	（ 相関係数 ＝ 0,9806 ）
4 〜 12/50分位	ｙ ＝ 5,990.7	ｘ ＋	196,293	（ 相関係数 ＝ 0.5492 ）
4,984.3		ｘ ＝	17,978
		ｘ ＝	3.61
よって		ｙ ＝	217,901

＜第５／５０分位付近で変曲点が存在すると仮定した場合＞

1 〜 5/50分位	ｙ ＝ 10,505	ｘ ＋	179,253	（ 相関係数 ＝ 0.9874 ）
5 〜 12/50分位	ｙ ＝ 6,316.3	ｘ ＋	193,146	（ 相関係数 ＝ 0.4888 ）
4,188.7		ｘ ＝	13,893
		ｘ ＝	3.32
よって		ｙ ＝	214,096

（図１）